1. 알고리즘 algorithm
알고리즘이란
•
어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법; 문제를 해결하는 방법
•
한 문제를 해결하는 방법은 한 가지만 있는게 아니라 무수히 많을 수 있다.
•
자주 쓰이는 문제 해결 방법(알고리즘)은 패턴화; BFS, DFS, DP, 다익스트라 등등
•
각 상황에 적합한 알고리즘을 선택할 수 있어야 한다.
알고리즘은 수학과 컴퓨터과학 분야에서 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법입니다. 알고리즘은 “문제를 해결하는 방법”이기 때문에 언어는 상관없습니다. 같은 원리에 따라 동작한다면 다른 언어로 작성되었더라도 같은 알고리즘을 사용했다고 볼 수 있습니다.
개발자는 현실의 문제를 해결하기 위해 코드를 작성하여 프로그램을 개발합니다. 한 문제를 해결하는 방법은 한 가지만 있는게 아니라 무수히 많을 수 있습니다. 그 중에서 자주 쓰이는 문제 해결 방법에는 BFS, DFS, DP, 다익스트라 등과 같이 이름을 붙여서 문제 해결 방법을 패턴화 하였습니다. 이렇게 패턴화된 문제 해결 방법을 보통 알고리즘이라고 부릅니다. 알고리즘을 학습하여 응용, 적용할 수 있게 된다면 비슷한 문제를 보다 쉽게 해결할 수 있습니다.
같은 문제상황에서도 개발자마다 해결 방법으로 내놓은 알고리즘이 다를 수 있습니다. 문제만 해결하면 되므로 아무 알고리즘으로 코드를 작성하면 될까요? 그렇지 않습니다. 문제를 해결할 수 있는 알고리즘이 여러 가지가 있더라도, 상황에 맞는 알고리즘을 잘 선택해야 합니다. 잘 선택할 수 있으려면 알고리즘을 평가할 수 있어야 합니다. 평가 기준에 대해서 간략히 살펴보도록 하겠습니다.
2. 알고리즘 평가기준
좋은 알고리즘이란
•
시간 복잡도
•
공간 복잡도
•
구현 복잡도
1.
시간 복잡도
적은 시간을 잡아먹는 알고리즘일수록 당연히 좋겠죠. 동일한 코드로 작성되어도 실행 환경에 따라서 매번 실행시간이 달라질 수 있습니다. 하지만 걸리는 시간의 경향성은 계산할 수 있습니다. 앞으로 배워볼 시간복잡도(Big-O)를 통해서 알고리즘마다 실행시간 경향성을 살펴보도록 하겠습니다.
2.
공간 복잡도 (메모리)
메모리는 한정적이기 때문에 최대한 적은 용량의 메모리를 사용하는 것이 좋습니다. 하지만 컴퓨터의 메모리 용량이 커짐에 따라서 메모리를 크게 신경쓰지 않고 알고리즘을 작성하는 경우도 있습니다. 공간복잡도를 통해 특정 알고리즘이 얼마만큼의 메모리를 차지하게 될 지를 나타냅니다.
3.
구현 복잡도
꽤 괜찮은 알고리즘을 떠올렸더라도 구현이 너무 복잡하고 알아보기 힘들다면 다시 생각해볼 필요가 있습니다. 개발자는 대부분의 경우 협업을 해야하고, 구현이 너무 복잡해지면 다른사람은 물론 미래의 나도 알아볼 수 없게 됩니다.
시간과 공간은 보통 trade-off 관계입니다. 꼭 그렇진 않지만, 실행시간을 줄이려면 메모리를 더 사용해야 하고, 메모리 사용량을 줄이려면 실행시간이 늘어나게 됩니다. 또한 실행시간이 적게 걸리고 메모리를 적게 차지하는 알고리즘이 무조건 좋은 것은 아닙니다. 결국 개발자가 알고리즘을 코드로 구현해야하는데, 너무 복잡한 알고리즘이라면 개발시간이 너무 늘어날 수 있습니다. 시간과 공간을 좀 더 차지하더라도 간단한 코드를 작성하는 편이 더 좋을 수 있습니다. 따라서 시간복잡도와 공간복잡도를 미리 계산하여 요구상황에 맞으면서도 간단한 알고리즘을 적절히 사용하는 것이 중요합니다.
한국 기업들의 알고리즘 코딩테스트에서는 공간보다는 시간을 더 중요하게 생각합니다. 메모리를 사용하더라도 실행시간을 줄이는 방법들을 강의에서 최대한 소개드리고자 합니다. 또한, 시간복잡도를 미리 계산하여 문제 조건을 딱 맞추면서도 가장 간단한 알고리즘으로 문제를 해결할 수 있도록 훈련을 해볼 것입니다.
3. 시간복잡도 Time Complexity
Runtime (실행 시간)
시간복잡도에 대해서 공부하기 전에, 실행시간(runtime)에 대해 알고 있어야 합니다. 우리는 코드를 한 줄 한 줄 작성하여 프로그램을 완성하죠. 그렇게 완성된 프로그램을 실행시키면 컴퓨터(CPU)는 한 줄 한 줄 코드를 처리하게 됩니다. 모든 코드를 처리하면 우리가 원하던 값을 얻을 수 있게 되고 프로그램은 끝나게 됩니다. 이렇게 프로그램이 시작되고 모든 코드를 실행하는데 걸리는 시간을 runtime(실행시간)이라고 합니다.
실행시간에 영향을 주는 요소는 크게 두 가지로 볼 수 있습니다.
1.
한 줄의 코드당 걸리는 시간
2.
프로그램 내 실행되는 코드의 갯수
CPU 1 tick당 걸리는 시간을 1 unit time이라고 해보겠습니다. 한 줄의 코드라고 해도 코드의 종류에 따라서 unit time은 다를 수 있습니다. 변수에 값을 대입하는 코드는 1 unit time이 걸리지만, 두 변수를 더한 값을 변수에 대입하는 코드는 3 unit time이 걸릴 수 있습니다. 입출력을 하는 코드라면 훨씬 더 많이 걸릴 수 있습니다.
int num1 = 100; // 1 unit time
int num2 = 50; // 1 unit time
int sum = num1 + num2; // 3 unit time
print(sum); // 100 unit time
C++
복사
이렇게 한 줄의 코드당 걸리는 시간은 모두 다를 수 있습니다. 그 차이가 크기도 합니다. 하지만 CPU입장에서는 큰 문제가 되지 않는 크기 입니다. 물론 정보올림피아드 대회같은 경우에는 한 줄의 코드에 걸리는 시간을 고려해야될 때도 있습니다. 하지만 코딩테스트에서는 이를 무시해도 충분합니다. 코딩테스트를 위한 알고리즘에서는 프로그램 내 실행되는 코드의 갯수만 신경쓰면 됩니다.
int sum = 0; // C1 unit time
sum += 1; // C2 unit time
sum += 2; // C3 unit time
sum += 3; // C4 unit time
sum += 4; // C5 unit time
sum += 5; // C6 unit time
print(sum); // C7 unit time
C++
복사
한 줄의 코드당 걸리는 시간은 무시해도 된다고 했으니 각각의 unit time을 C1, C2, ... , C7 unit time로 표현을 해보겠습니다. 코드의 갯수를 세보면 7개의 코드가 있다고 생각하면 되겠네요. 하지만 이것도 CPU입장에서는 매우 적은 숫자에 불과합니다. 1개의코드가 있든, 7개의 코드가 있든 순식간에 계산을 해버리죠. 그래서 적은 갯수의 코드 또한 하나로 묶어서 봐도 상관없습니다. CPU입장에서는 1 unit time이든 100 unit time이든 상관없으니 그냥 하나로 묶어서 상수(Constant)시간 C unit time으로 표현합니다.
하지만 코드의 갯수가 100개가 아니라 1,000,000개면 어떨까요? 1,000,000,000개면 무시할만 할까요? 점점 CPU입장에서도 시간이 많이 걸리기 시작합니다. 이렇게 시간이 많이 걸리는 코드는 보통 반복문에 숨어 있습니다.
int sum = 0;
for(int i = 0; i < 10000000; i++){
sum += 1;
}
print(sum)
C++
복사
3~5번째 줄의 for 반복문을 보면 3줄밖에 되지 않는 코드같지만, 실제로는 10,000,000번 실행되는 코드입니다. 측정해본 결과 해당 프로그램이 작동되는 시간은 약 38ms(0.038s) 정도 걸리네요. 만약 반복횟수가 x10번 더 실행되는 반복문이라면(100,000,000번 실행) 실행시간도 대략 x10정도(207ms)로 늘어납니다.
반복횟수에 따른 runtime 증가 추이
그래도 다행인건 이렇게 반복문의 반복 횟수가 정해져 있는 경우는 실행시간이 어느정도 걸릴지 예상이 가능하다는 것입니다. 하지만 예상을 할 수 없는 상황도 있습니다.
int sum = 0;
int n = 0;
input(n);
for(int i = 1; i < n; i++){
sum += i;
}
print(sum);
C++
복사
의 값을 사용자로부터 받는 경우에는 반복문이 몇회 반복될지 예상할 수 없겠죠. 실행시간을 계산할 때, 이 작은 숫자라면 무시해도 되지만, 의 굉장히 큰 숫자라면 무시할 수 없습니다. 이처럼 입력 에 따라서 실행시간이 변하는 경우 runtime을 에 대한 함수로 표현할 수 있습니다.
여기서 중요한 것은 입력된 의 값에 따라 실행시간이 변한다는 것입니다. 따라서 우리가 작성한 코드의 실행시간을 짐작하기 위해서는 을 잘 관리하는 것이 중요합니다. 입력값 n 이외의 상수시간이 걸리는 코드들은 다 묶어서 C unit time으로 퉁치면 됩니다.
runtime의 다양한 예제를 보도록 하겠습니다.
printf('hi'); // C unit time
C++
복사
for(int i = 0; i < 100; i++){
printf('hi'); // C1 unit time
}
C++
복사
for(int i = 0; i < 100; i++){
for(int j = 0; j < 100; i++){
printf('hi'); // C1 times
}
}
printf('bye'); // C2 times
C++
복사
for(int i = 0; i < n; i++)
{
printf('hi'); // C1 times
}
printf('bye'); // C2 times
C++
복사
for(int i = 0; i < n; i++)
{
for(int j = 0; j < 1000; j++)
{
printf('hi'); // C1 times
}
}
printf('bye'); // C2 times
C++
복사
for(int i = 0; i < n; i++){
for(int j = 0; j < n; i++){
printf('hi'); // C1 times
}
printf('bro'); // C2 times
}
printf('bye'); // C3 times
C++
복사
시간복잡도
시간복잡도는 문제를 해결하는데 걸리는 시간과 입력값 의 함수 관계를 말합니다. 그렇다면 왜 시간복잡도가 필요할까? 그 이유는 내가 고안해낸 알고리즘으로 작성한 코드가 얼마만큼의 실행시간이 걸릴지를 예상하기 위해서입니다. 시간복잡도를 미리 계산할 수 있다면, 키보드로 코드를 모두 작성하여 실행시키지 않아도 얼추 실행시간을 예측할 수 있습니다. 실제 개발을 하다보면 1초안에 어떤 작업들을 처리할 수 있는 프로그램을 작성해야 하는데, 이때 시간복잡도를 계산하지 못하면 생각나는 모든 알고리즘을 직접 작성하고, 시간을 비교해야하는 비효율이 발생합니다. 하지만 시간복잡도를 계산할 줄 안다면, 상황에 맞는 알고리즘을 고안해낼 수 있습니다.
코딩테스트에서는 시간복잡도가 굉장히 중요합니다. 단순히 코드 구현력을 묻는 문제들도 많지만, 알고리즘적 사고능력을 묻는 문제들은 시간복잡도 계산을 하여 효율적으로 코드를 작성할 수 있는 개발자를 변별하기도 합니다. 따라서 문제가 주어지면 바로 키보드를 잡지말고 시간복잡도부터 계산한 후 어떤 알고리즘으로 문제를 풀 것인지를 결정하여야 합니다.
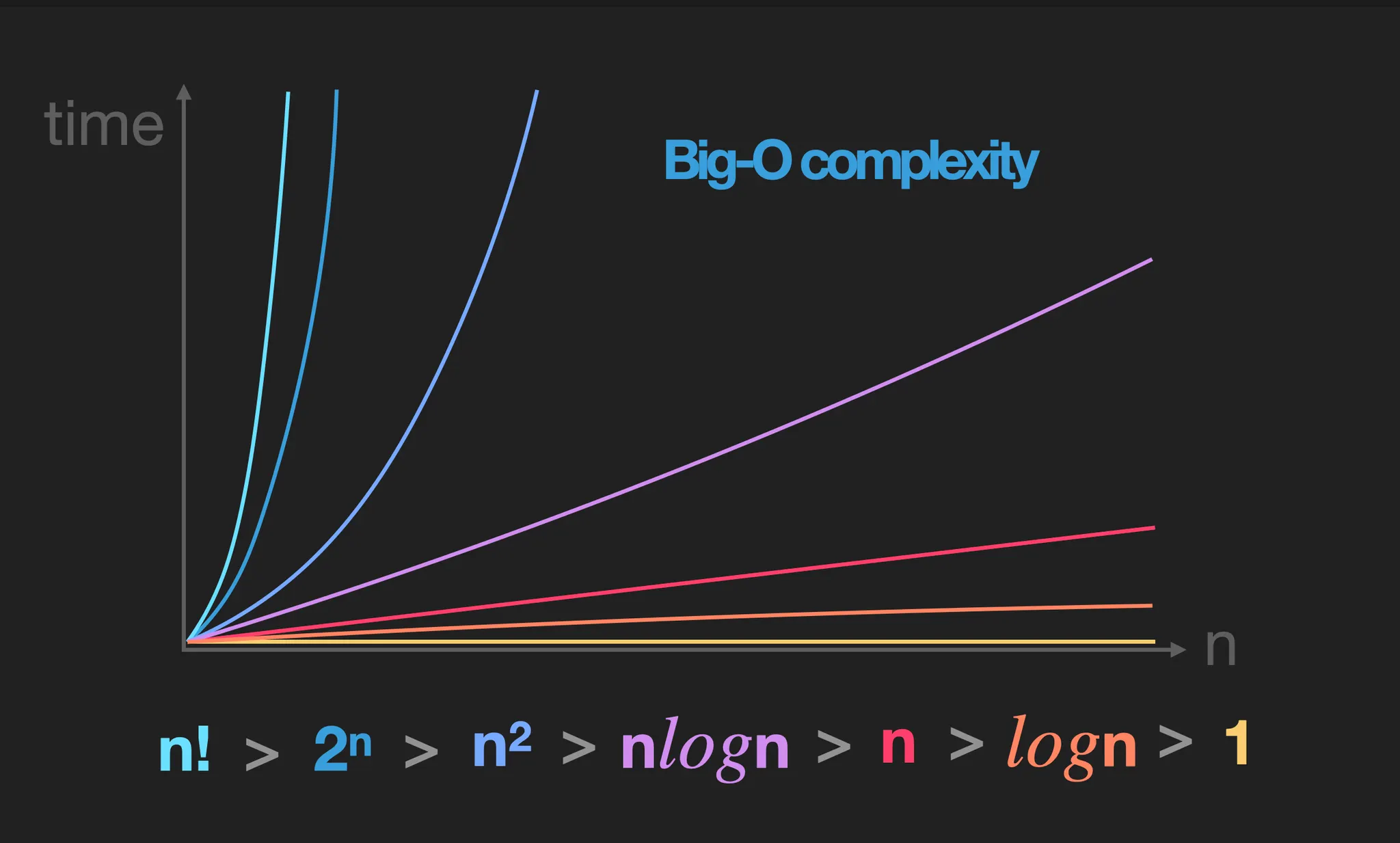
시간복잡도는 우리가 지금까지 익혔던 값을 토대로 “Big-O notation”으로 표현합니다.
Big-O
input 의 크기가 커지면 작은 차수의 항들이 runtime에 미치는 영향이 미미하다
⇒ 작은차수 무시, 계수 무시
예시를 들어 설명드리겠습니다.
의 크기가 작다면 모든 항들이 고만고만할 것입니다. 예를들면 입력값 n이 10이면, 다음과 같은 결과가 나옵니다.
여기서 입력값 의 크기가 굉장히 크다고 가정하면 의 영향력이 굉장히 커질 것입니다. 이와 반면 과 그리고 상수항은 영향력이 미미해질것입니다. 위의 식에서 의 값에 1,000을 대입해 보면 더 쉽게 알 수 있습니다. 은 1,000,000,000이 되는 반면에 은 고작 1,000밖에 안된다. n의 차수가 커질 수록 격차가 커집니다.
Big-O는 이러한 계산 결과를 단순화 하기 위해서 최고차항을 제외한 항들은 모두 무시합니다.
Big-O를 적용하기 위해서는 최고차항이 무엇인지 판별을 해야되는데, 기본적인 것들은 외우고 계시면 편합니다.
간단한 코드들을 보면서 Big-O 감을 익혀보도록 하겠습니다!
a = 5
a += 1
Python
복사
simple statements
for i in range(n):
print("hi")
Python
복사
single loop
for i in range(n):
for j in range(n):
print("hi")
Python
복사
nested loop
int fibo(int n)
{
if (n == 1)
return 0;
else if(n == 2)
return 1;
else
return fibo(n - 1) + fibo(n-2);
}
C++
복사
int binarySearch(int data[], int n, int target)
{
int start = 0;
int end = n;
int mid;
while (end >= start)
{
mid = (end + start) / 2;
if (data[mid] == target)
return 1;
else if (data[mid] > target)
end = mid - 1;
else
start = mid + 1;
}
return 0;
}
C++
복사
탐색해야되는 데이터가 절반식 줄어드는 함수
ex) 이진탐색 알고리즘
worst-case
Big-O notation을 이용하여 시간복잡도를 구할 때에는 최악의 상황(worst-case)를 고려해야 합니다.
# O(n)
if condition:
for i in range(n):
pass
# O(n^2)
else :
for i in range(n):
for j in range(n):
pass
Python
복사
위의 코드에서 보통의 경우 if문이 실행되고, 굉장히 가끔 else문이 실행된다고 가정해 보겠습니다. 그렇다면 최악의 경우(else문이 실행되는 상황)의 시간복잡도는 이기 때문에 위의 코드의 시간복잡도는 이다.
4. 코딩테스트를 위한 시간복잡도
외우면 편한 것들
1.
sort()
몇몇 문제는 정렬을 하면 쉽게 해결할 수 있습니다. 하지만 우리는 정렬을 직접 구현하지 않을 것이고, 각 언어에서 정의되어 있는 의 sort() 함수를 사용할 것입니다.
2.
Hashtable 구축 : // Hashtable 검색 :
Hashtable의 강력함은 검색의 시간복잡도가 라는 점입니다. 사실 hashtable은 공간(메모리)를 사용함으로써 시간을 절약하는 방법중에 하나입니다.
보통 문제에서 주어지는 크기 의 데이터(배열의 형태)에 하나 하나 접근하여 hashtable을 구축해야 합니다. 이 과정에서 의 시간복잡도가 걸립니다.
3.
Binary Search ⇒
정렬된 배열에서 특정 숫자를 찾는 알고리즘인 Binary search는 코딩테스트 문제에서도 종종 나온다. 반복문 또는 재귀 함수가 재호출 될 때마다 탐색해야할 데이터의 크기가 절반씩 줄어들기 때문에 시간복잡도는 이 된다.
만약 정렬이 안된 배열이 주어졌다면, 정렬 을 먼저 해주어야 한다.
4.
Heap (priority queue)
•
길이가 n인 배열을 heap으로 만들 때 ⇒
•
push() ⇒
•
pop() ⇒
문제에 적용하는법
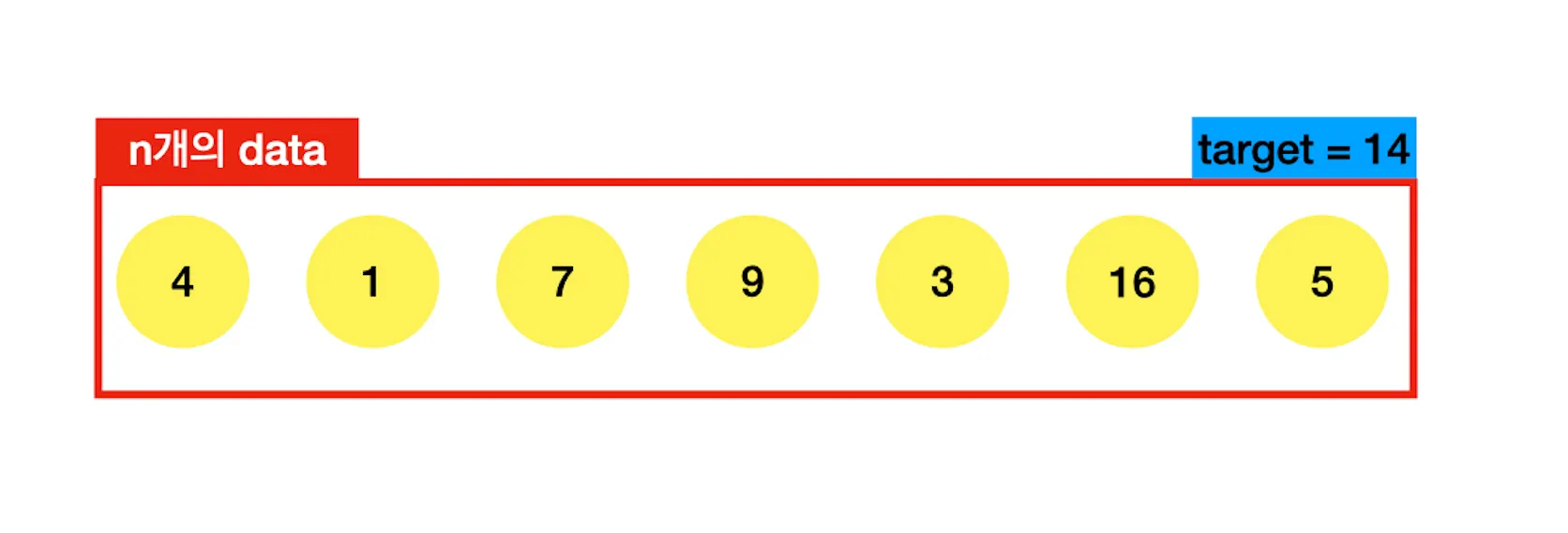
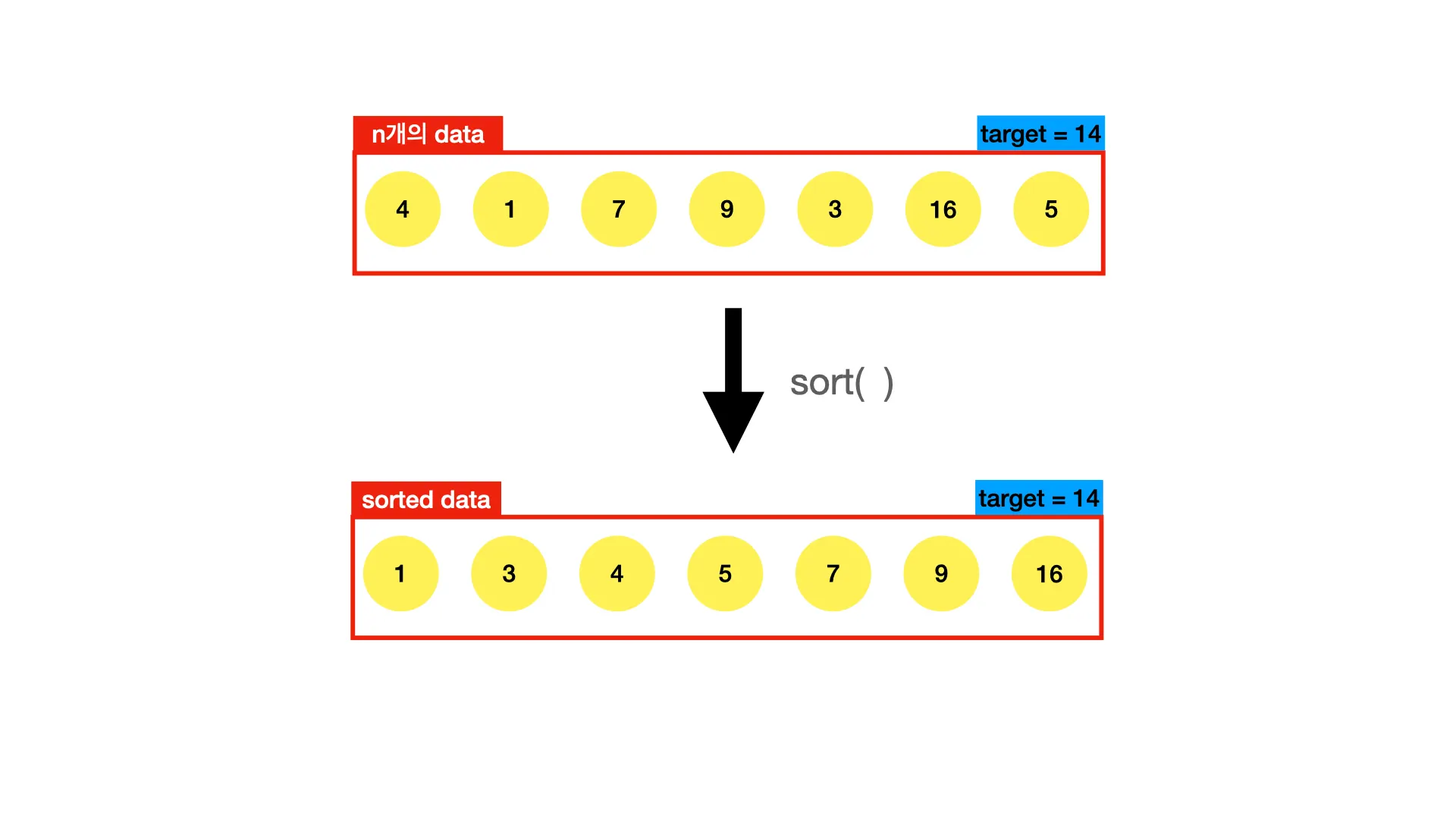
문제를 간단히 설명드릴게요.
n개의 정수가 저장되어 있는 배열이 하나 주어진다. 배열의 원소를 두 개 더해서 target number가 될 수 있다면 True, 불가하면 False를 반환 해라
풀이 방법
1.
완전탐색(Brute-force)
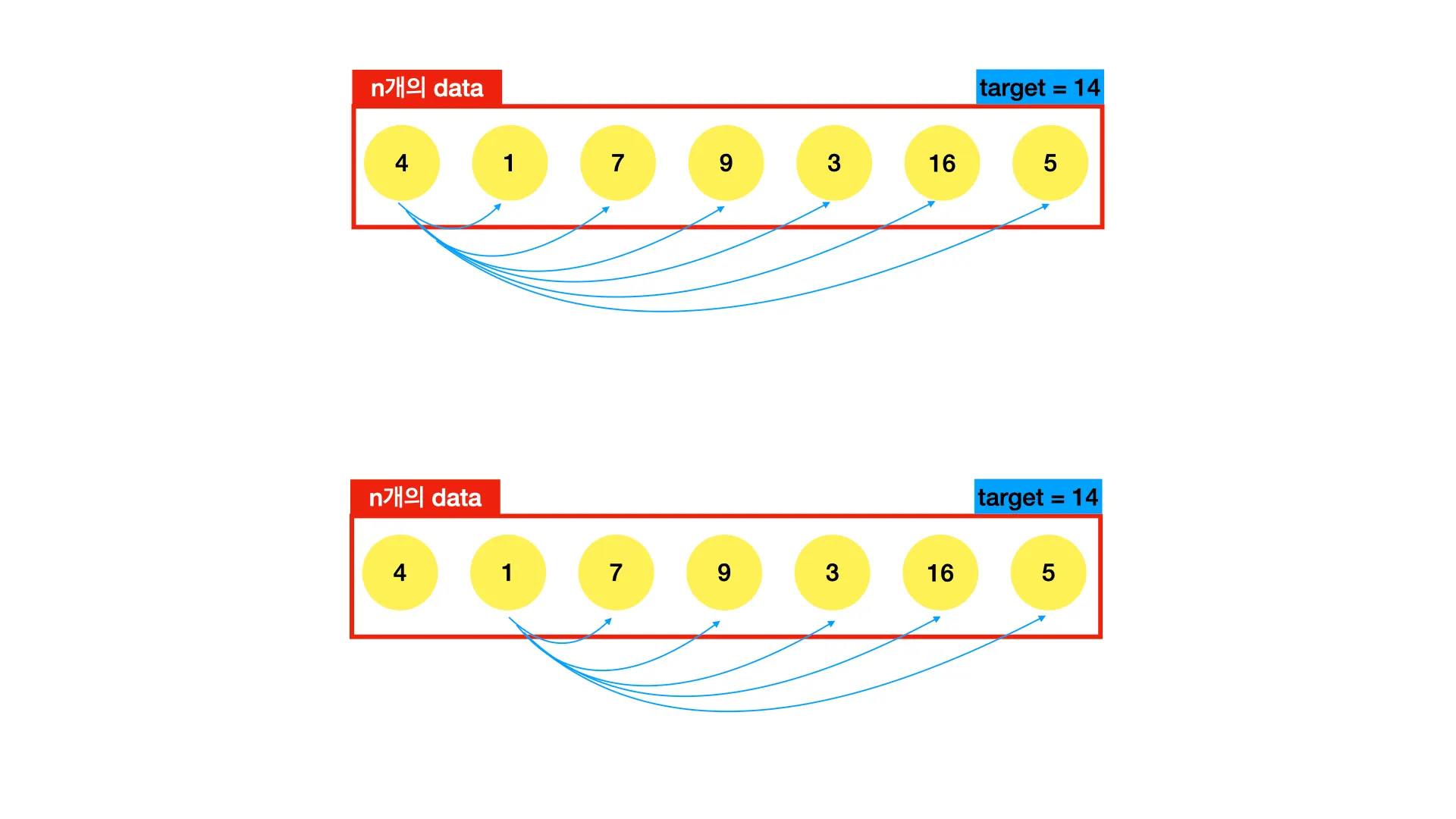
가장 직관적인 풀이 방법은 완전탐색입니다. 완전탐색은 간단히 말씀드리면 "무식하게 일일이 다 해보기" 라고 생각하면 됩니다.
첫 번째 원소를 선택해서 다른 원소들과 일일이 더해봅니다. target = 14와 동일한 값이 나오면 True를 반환합니다.
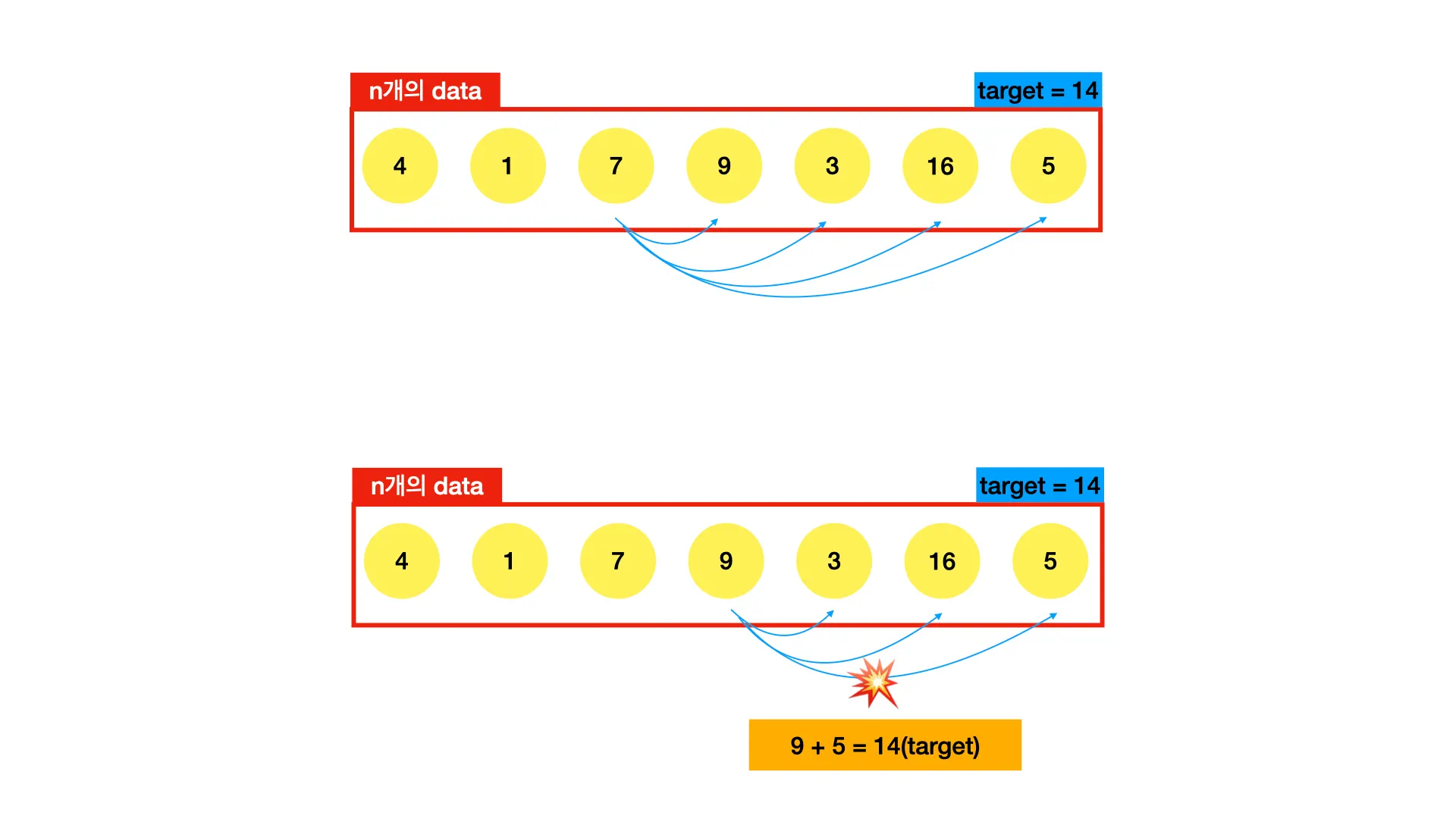
첫 번째 원소에 대해서 일일이 다 해봤으면, 두 번째 원소에 대해서 일일이 해봅니다. 이 과정을 반복합니다.
4번째 원소 9와 7번째 원소 5를 더했을 때 14가 나오네요. True를 반환합니다.
이를 코드로 작성해보면 다음과 같습니다.
def twoSum(nums, target):
for i in range(len(nums)):
for j in range(i+1, len(nums)):
if nums[i] + nums[j] == target:
return [i, j];
Python
복사
시간복잡도는 이고, 여기서 은 nums 배열의 size입니다.
즉 nums 배열의 크기 이 커지면 실행시간은 의 크기로 커집니다.
2.
정렬
데이터를 정렬시키면 좀 더 효율적인 알고리즘을 구상할 수 있는 경우가 종종 있습니다. sort(), heap, binary search 등을 이용하면 좀 더 효율적인 알고리즘으로 해결할 수 있는지 생각해보면 좋습니다.
이 문제는 정렬을 하면 완전탐색 보다 효율적인 알고리즘으로 풀이를 할 수 있다.
위의 알고리즘은 정렬된 데이터를 이용하는 것이다. 제일 먼저 정렬을 하기위해 sort()메서드 를 사용했다.
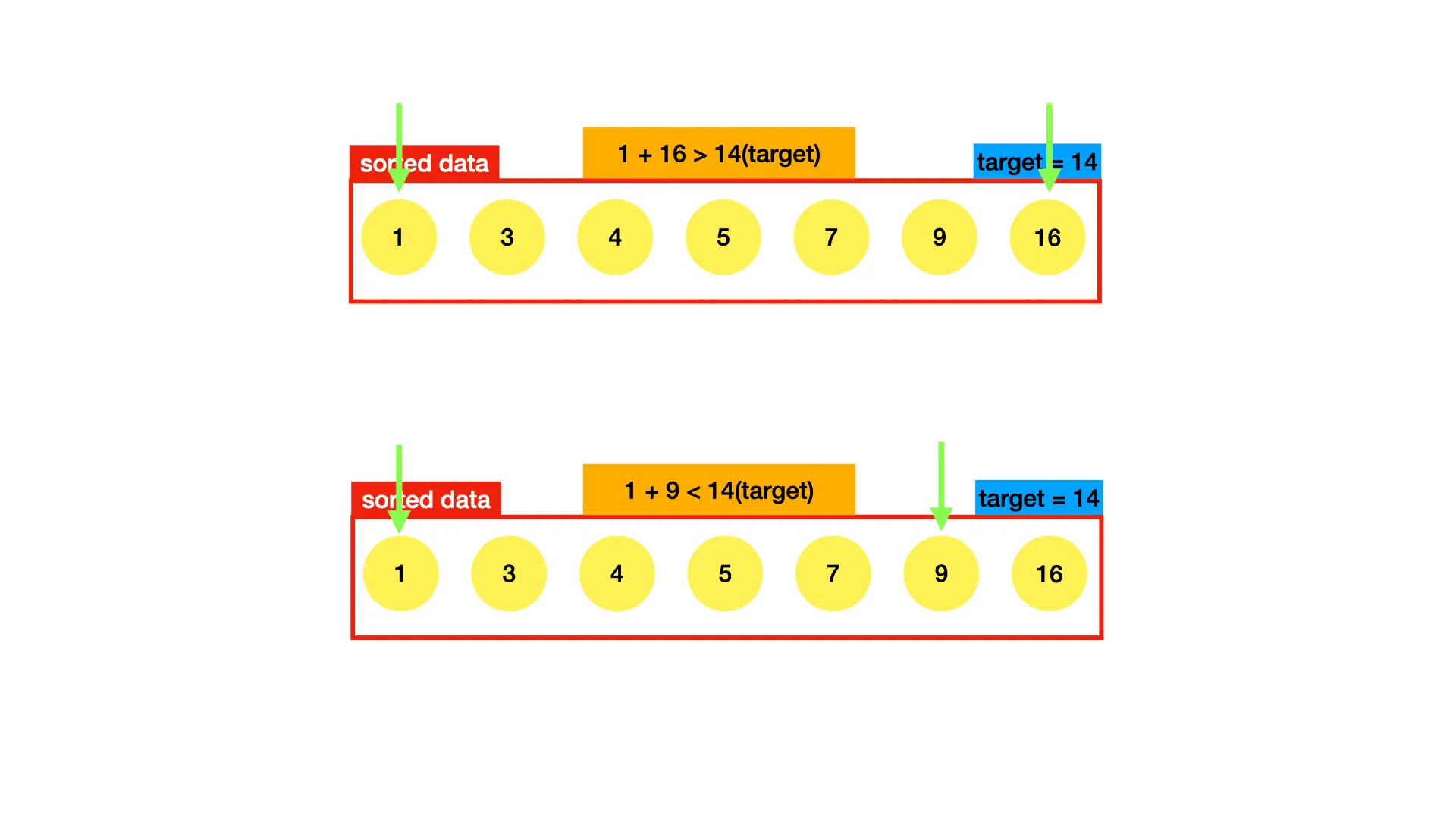
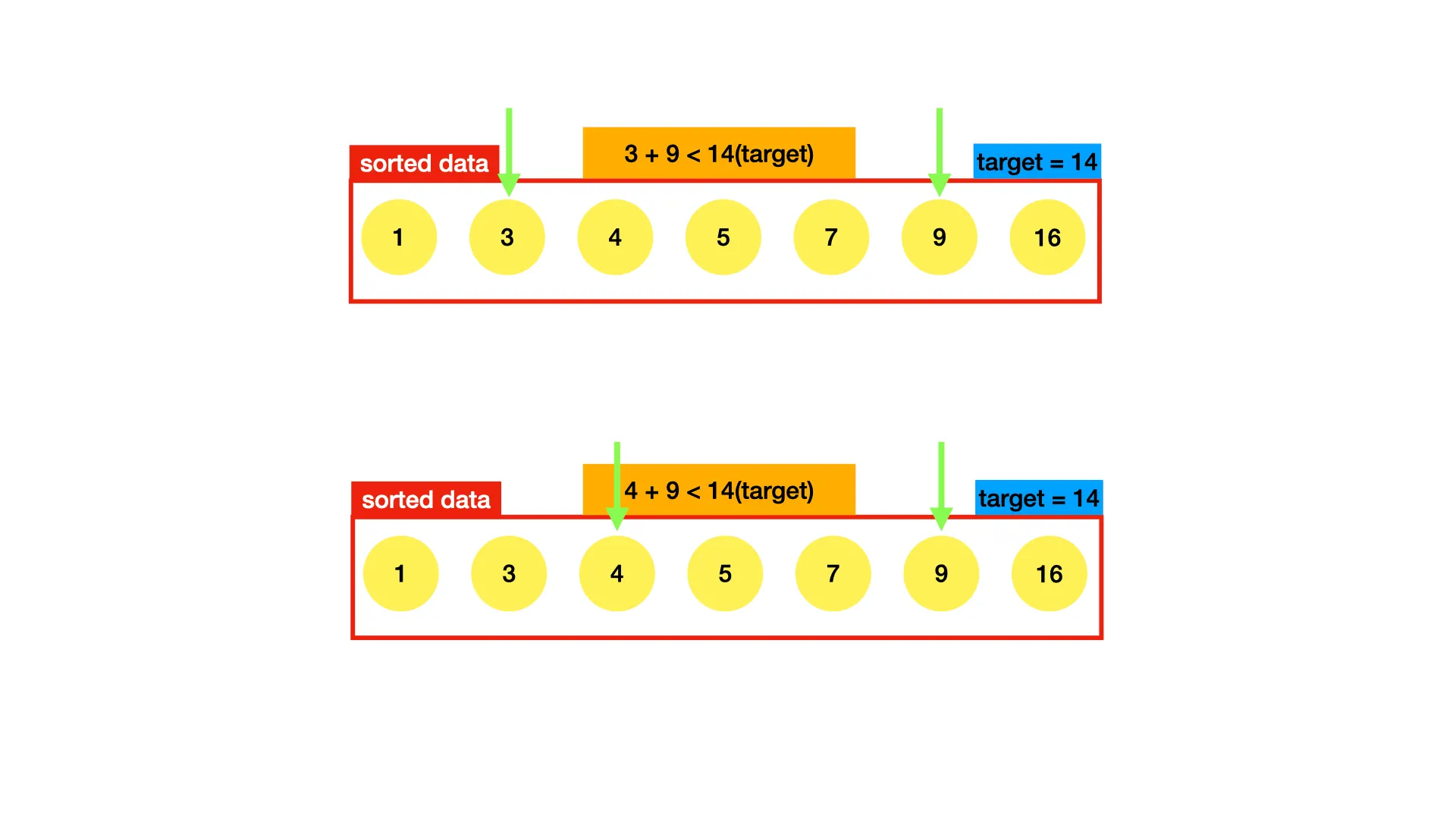
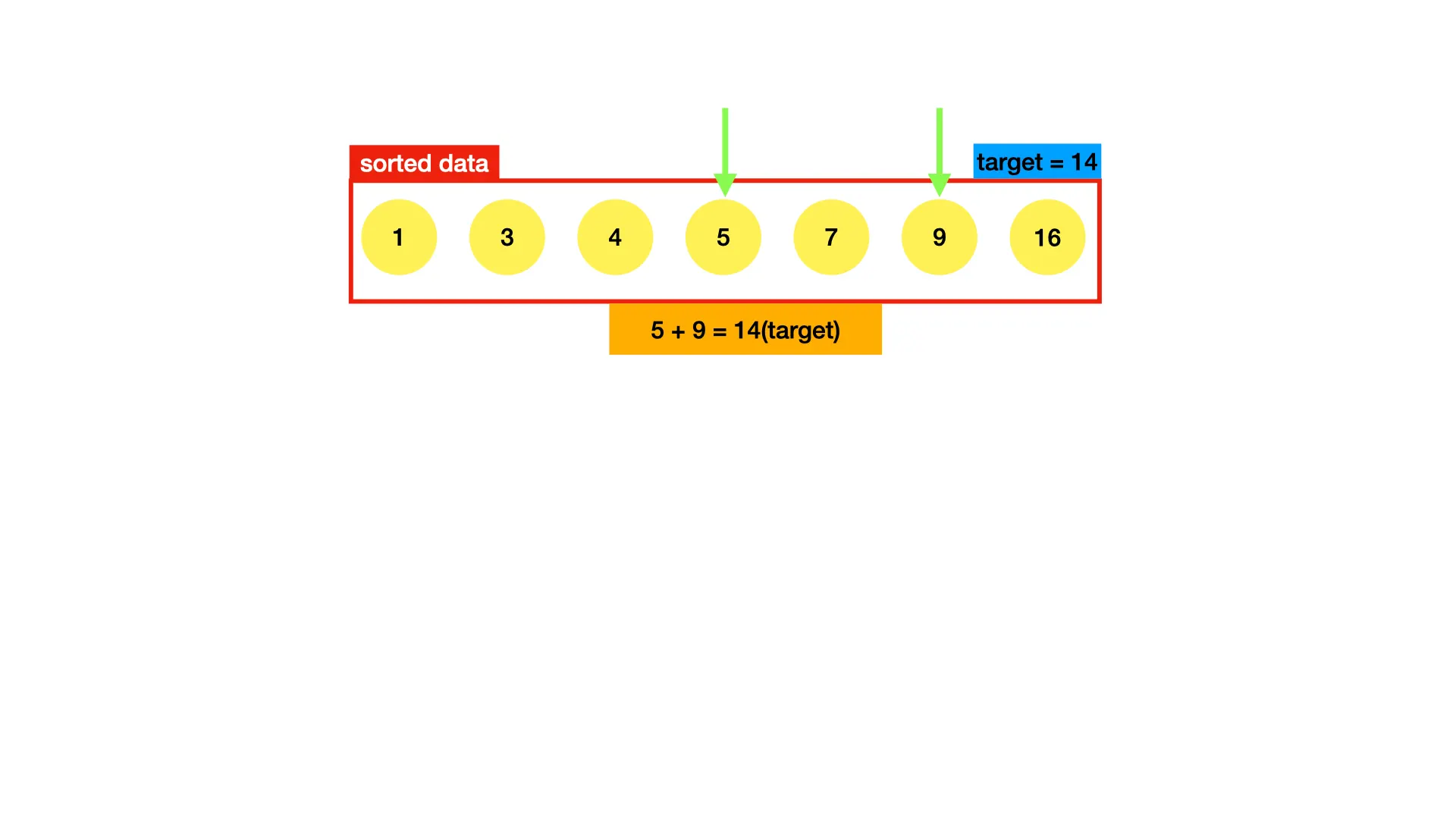
⇒
정렬된 데이터의 양 끝 index에 있는 두 숫자를 더한 값이 target보다 크면 오른쪽 index를 한 칸 왼쪽으로 옮기고, target보다 작으면 왼쪽 index를 한 칸 오른쪽으로 옮긴다. 이를 target과 같아질 때까지 반복한다.
⇒
'''
정렬 O(nlogn)
'''
def twoSum(nums, target):
# O(nlogn)
nums.sort()
l, r = 0, len(nums)-1
# O(n)
while l < r:
if target > nums[l] + nums[r] : l += 1
elif target < nums[l] + nums[r] : r -= 1
else: return True
return False
Python
복사
이 알고리즘의 시간복잡도는 이다. 부분부분 시간복잡도를 구하더라도, 전체적인 시간복잡도는 가장 차수가 높은 시간복잡도에 맞춰진다(Big-O notation)
이렇게 정렬을 활용하여 완전탐색보다 효율적으로 문제를 풀 수 있었다. 알고리즘 문제를 풀다보면 과 이 굉장히 큰 차이라는 것을 알게 될 것이다.
3.
메모리를 사용하여 시간효율을 극대화!
메모리를 잘 사용하면 시간효율을 높일 수 있다. 메모리를 잘 활용한다는 것은 자료구조를 적재적소에 사용한다는 것이다. 배열로 들어온 데이터를 트리나 그래프등으로 변환한 후 문제를 푸는 방식도 있을 것이다. 그 중에서도 가장 자주 사용되고 효과가 굉장히 좋은 것은 hashmap을 사용하는 것이다.
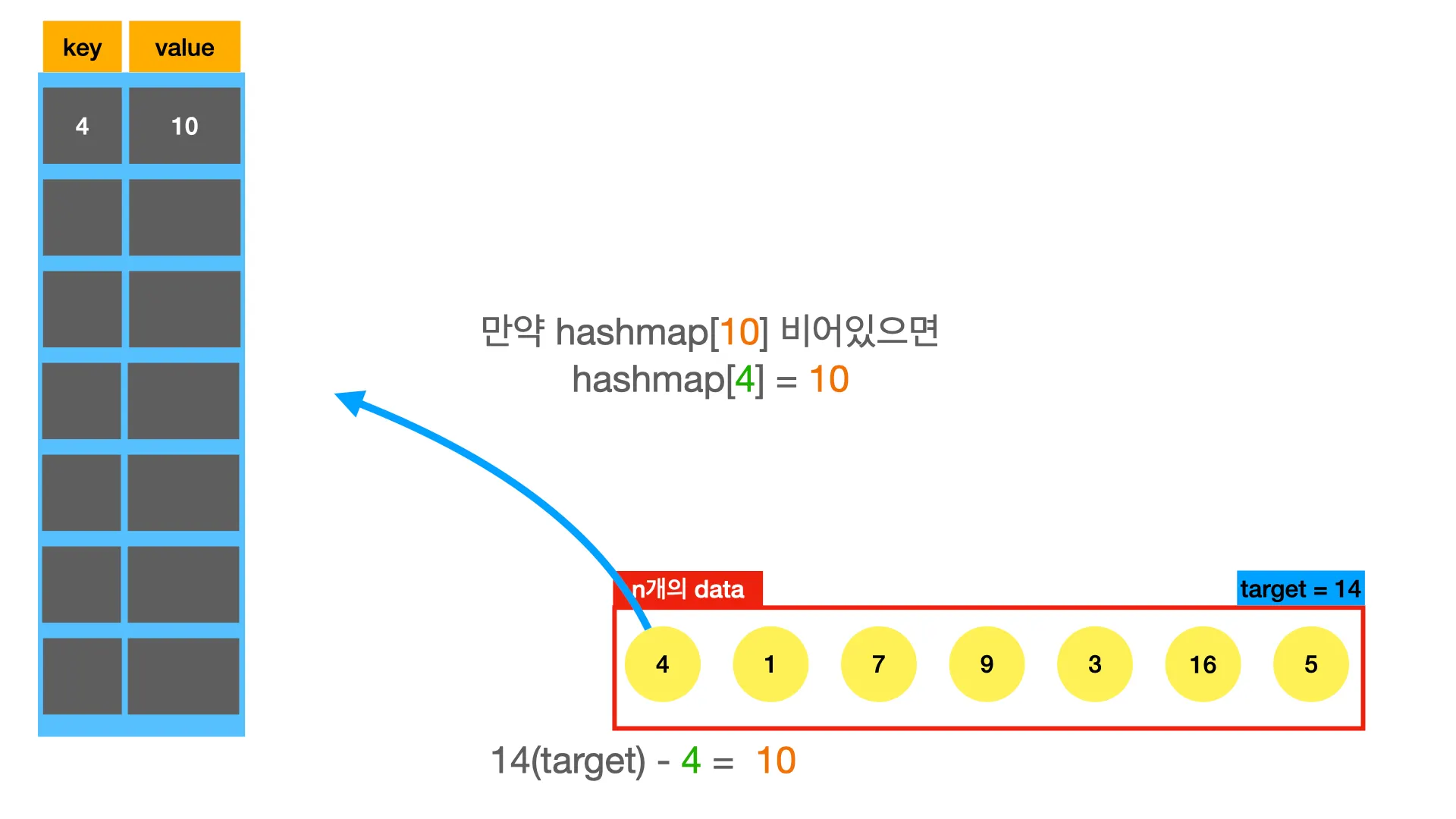
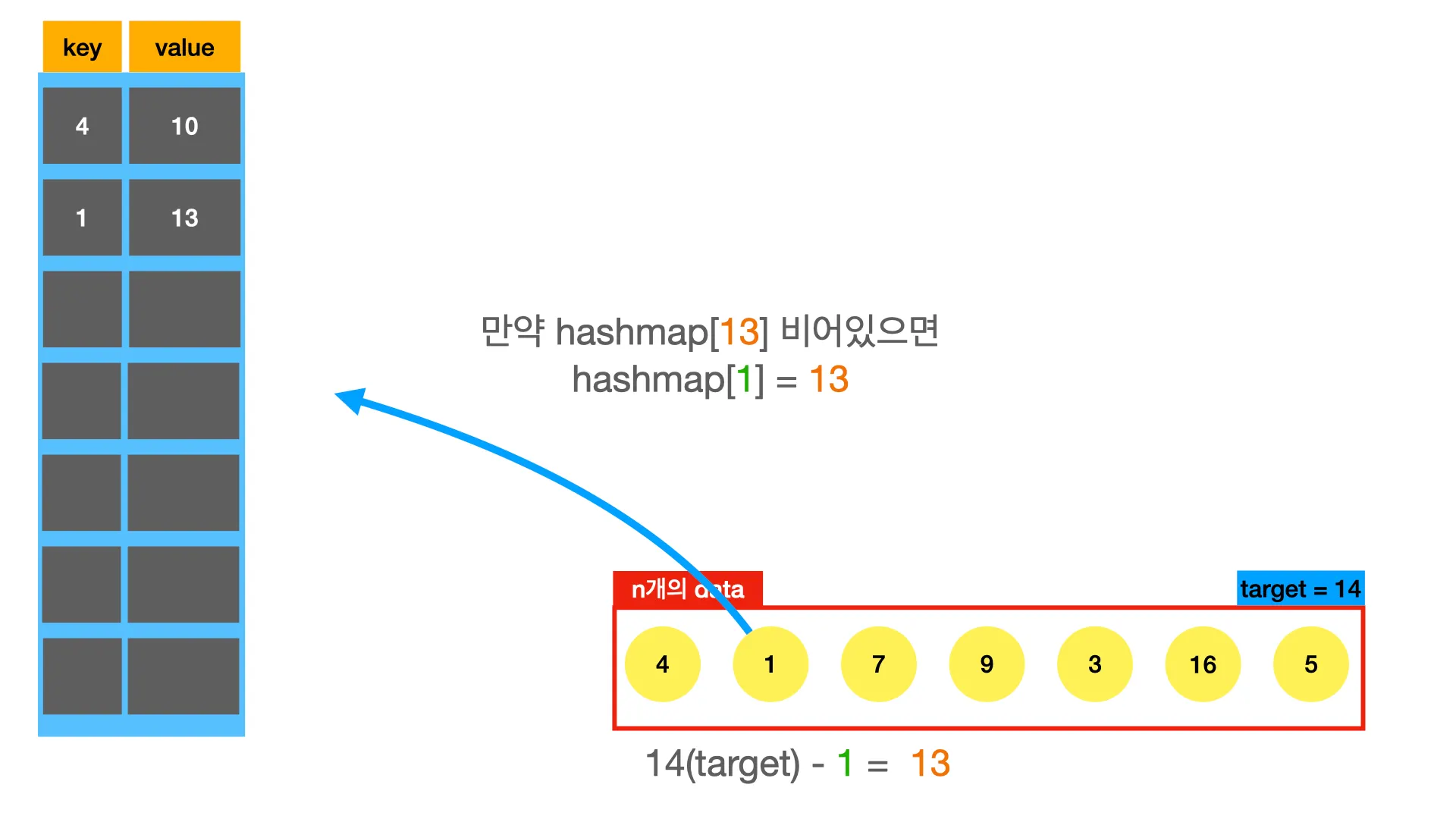
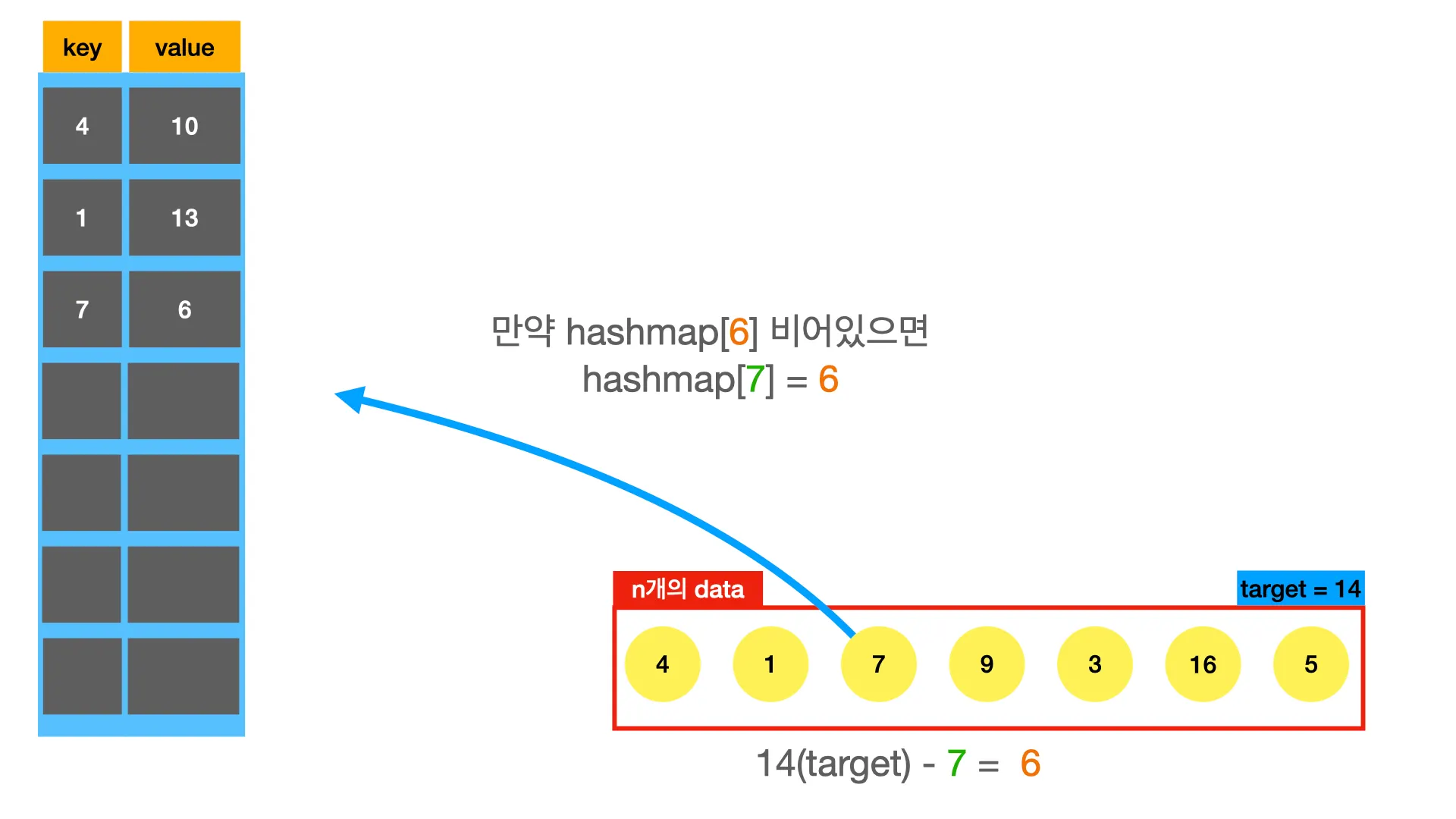
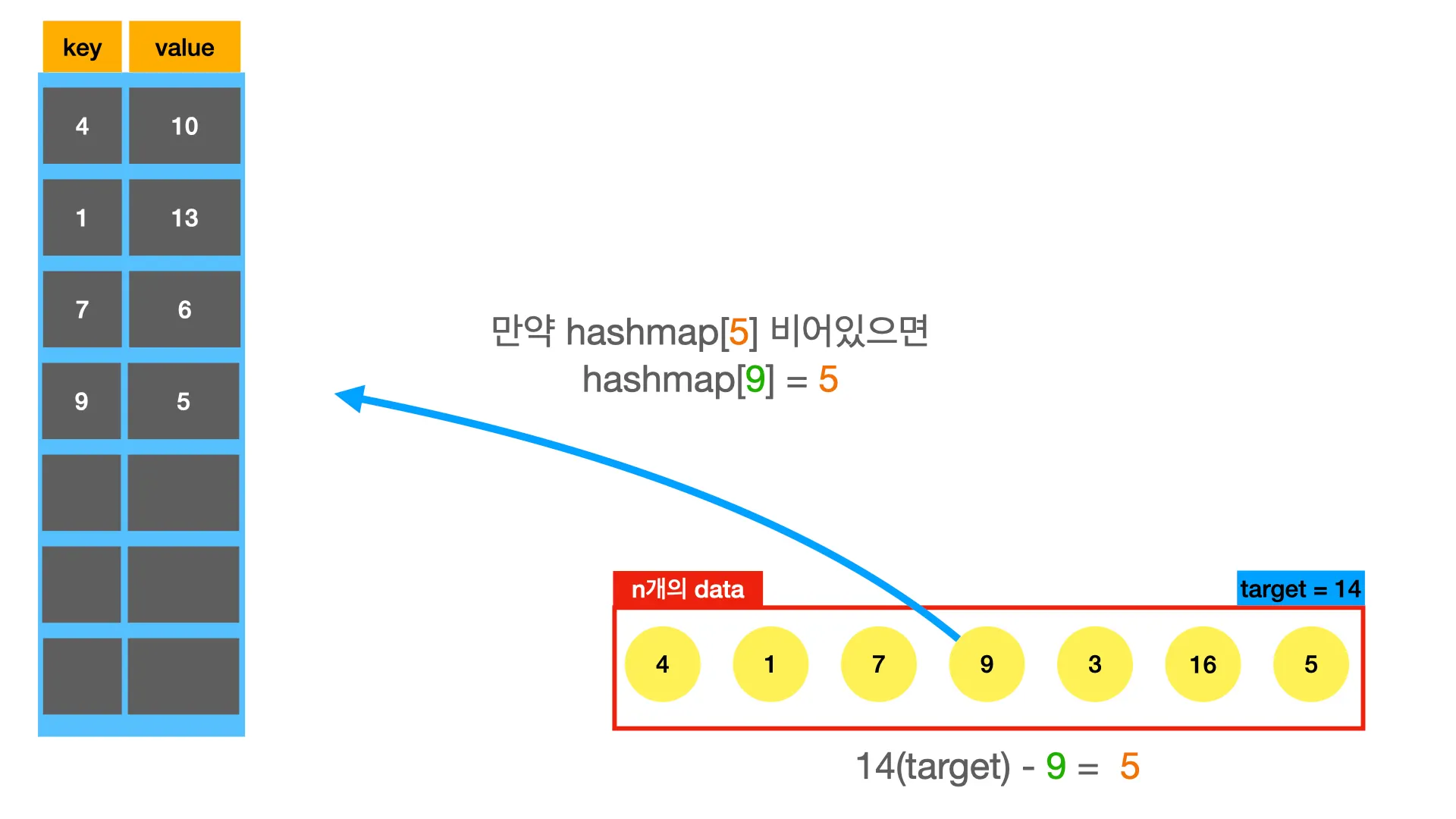
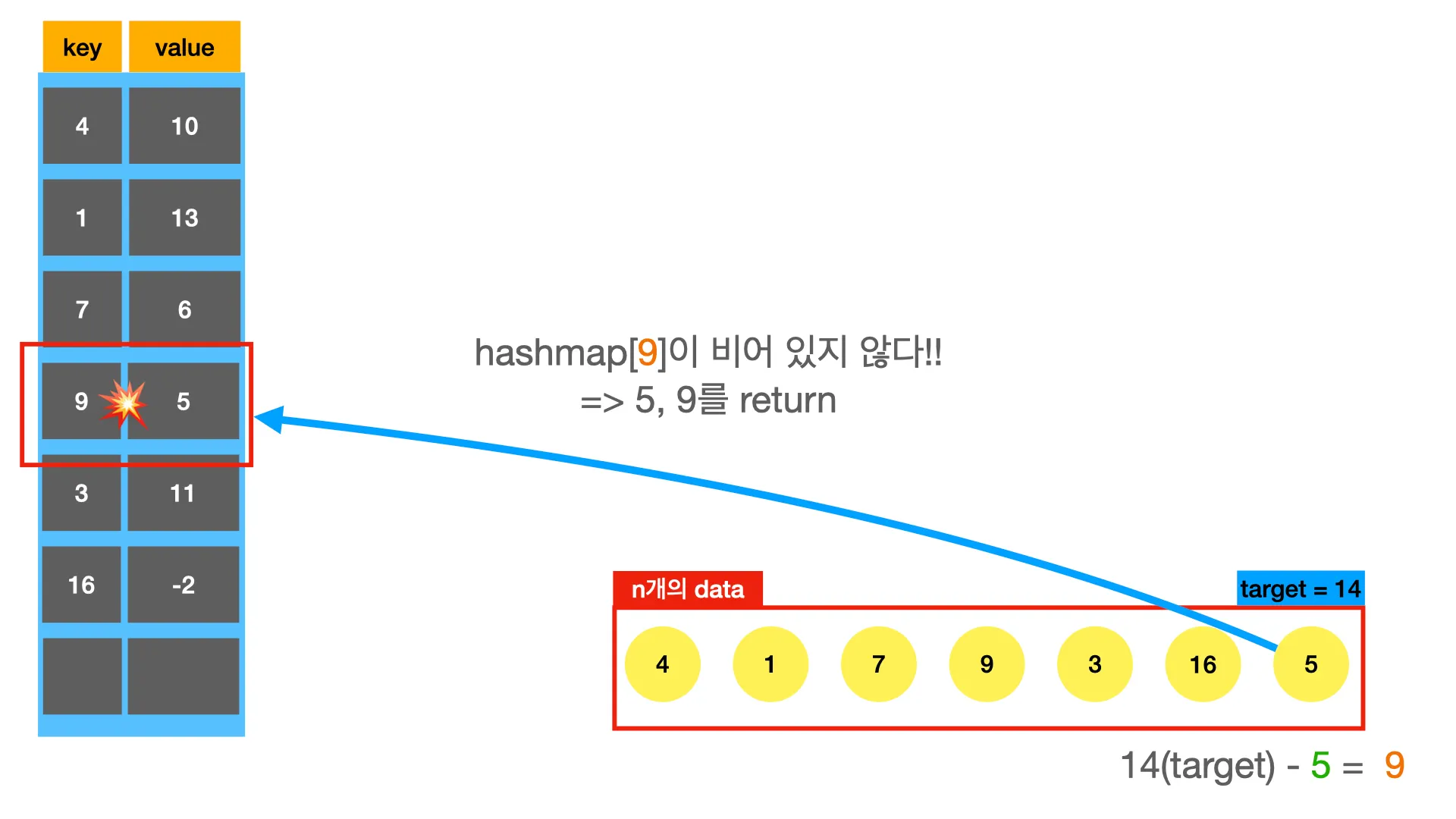
twosum문제도 hashmap을 적용해보자.
—- 중간 생략 —-
'''
hashmap 이용 O(n)
'''
if i in num(arr):
o(n)
def twoSum(nums, target):
seen = {} # 비어있는 hashmap 선언
for i, v in enumerate(nums):
complement = target - v
if complement in seen:
return [seen[complement], i]
else
seen[v] = i
return False
Python
복사
hashmap은 로 접근할 수 있기 때문에, 메모리가 충분하고 hashmap을 만드는데 시간이 오래걸리지 않으면 굉장히 강력한 도구가 된다. 보통 n개의 데이터로 hashmap을 만들어야 하기 때문에 만드는 과정에서 의 시간이 든다.
위의 풀이에서도 반복문을 한번 돌면서 모든 과정을 마쳤다. 따라서 시간복잡도는 이다.
앞으로 문제를 많이 풀어야 할 것이다. 문제를 풀 때마다, 시간에 너무 집착하고 정답을 맞추는 것에만 혈안이 되면 얻는것이 너무 적다. 키보드를 잡기전에 계획부터 해보자. 시간복잡도를 계산을 하고 비효율적인 알고리즘부터 효율적인 알고리즘까지 직접 코드를 작성해보자.
이런 훈련이 코딩테스트를 준비할 때 굉장히 유용하다. 왜냐하면 코딩테스트에서는 어렵고 복잡한 알고리즘을 알고있는지 물어보는 것이 아닌, 시간효율을 따져가며 구현을 잘 해낼 수 있는지를 주로 물어보기 때문이다.
코딩테스트에서 활용하기
시간복잡도를 계산해가면서 문제를 푸는 이유는 무엇일까. 코딩테스트에서 시간복잡도를 물어보기 때문이다!! 이제부터 우리가 배운 시간복잡도를 어떻게 코딩테스트에서 활용하는지를 살펴볼 것이다.
시간복잡도(Big-O)에 데이터의 크기(n)를 넣어서 나온 값이 100,000,000(1억) 이 넘으면 시간 제한 초과할 가능성이 있다!
runtime을 간단히 표현한게 시간복잡도이다. 따라서 시간복잡도에 데이터의 크기 n 을 넣으면 대략적인 runtime(실행시간)을 구할 수 있다. 이렇게 구한 수치가 너무 크다면 시간 제한 초과가 될 수 있다. 따라서 우리가 생각해낸 알고리즘을 실제로 코드로 작성하고 실행시키기 전에 시간 제한 초과가 발생할 지, 발생하지 않을 지 예상을 해야한다. 문제를 보자.
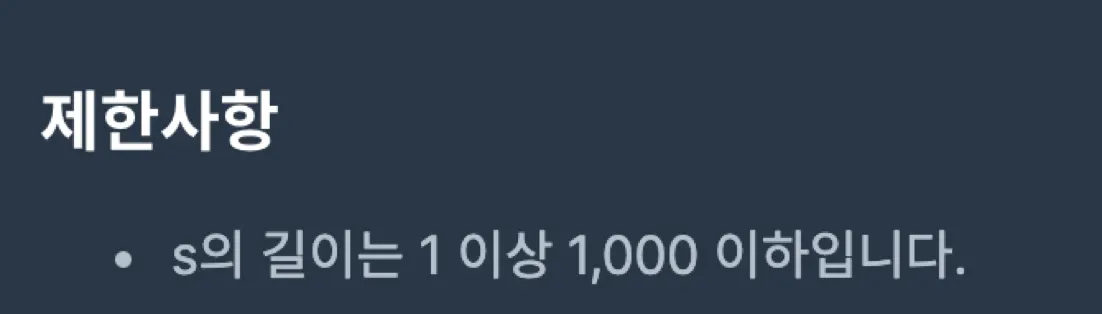
제한조건
1.
100,000
문제를 풀다보면 제한사항에 데이터의 크기를 100,000으로 제한한 문제들을 자주 보게 될 것이다.(직접 찾아보자). 100,000이라는 숫자에 숨겨져있는 뜻은 다음과 같다.
⇒ 로 풀기는 위험하다
⇒ , , 의 알고리즘을 생각해야 한다.
문제: 완주하지 못한 선수
# 완전탐색 O(n^2)
# 제한사항 100,000
# 알고리즘 개선 => sort, hashmap
def solution(completion, participant):
comp.sort()
part.sort()
for i in enumerate(comp):
if comp[i] != part[i]:
return part[i]
return part[-1]
# hashmap
Python
복사
2.
3.
데이터의 크기 제한이 작다면 완전탐색 고려!
완전탐색은 무식하게 일일이 다 해보는 방식이기 때문에 시간복잡도가 굉장히 큰 경우가 많다. 하지만 문제에서 데이터 크기 제한이 작다면, 완전탐색으로 풀어도 된다는 무언의 힌트인 것이다. 가장 생각해내기 쉬운 완전탐색 알고리즘으로 문제를 풀어도 된다는데 마다할 이유가 있을까
문제: 자물쇠와 열쇠
⇒ 으로 4중 반복문이 나와도 그냥 그러려니 하고 풀면 된다. 범위가 작으니까!!
⇒ 이 문제의 풀이방식이 떠올랐을 때, 시간초과가 날까봐 잔뜩 긴장했다. 하지만 제한사항을 보고나서 확신을 갖고 무식한 방법을 밀어붙여서 결국 문제를 해결할 수 있었다. 만약 시간복잡도를 미리 계산하지 못했다면 문제를 풀다가 '이렇게 풀어도 되는건가..?' 하고 확신을 잃었을 것이다.
4.
순열조합 완전탐색 문제
순열조합 문제는 완전탐색의 연장선상에 있다. 순열조합 문제는 시간복잡도가 굉장히 크기 때문에 작은 크기의 제한사항을 준다.
문제: 소수찾기
⇒ 으로 풀어도 된다.
⇒ 이정도 크기의 제한사항을 보면 직감적으로 알 수 있다. 완전탐색, 그중에서도 순열조합을 쓰면 되겠구나!
모든 문제에 제한사항이 있는 것은 아니다. 어떤 문제들은 시간효율은 상관없이 단순 구현만 요구하는 경우도 많다. 하지만 제한사항 하나에도 이런 숨겨진 의도가 있다는 것을 알고 있으면 코딩테스트에서 큰 무기가 될 것이다.
Copyright. 노씨데브. All rights reserved. 무단 공유 및 배포를 금합니다.